PRNG Relative Performance

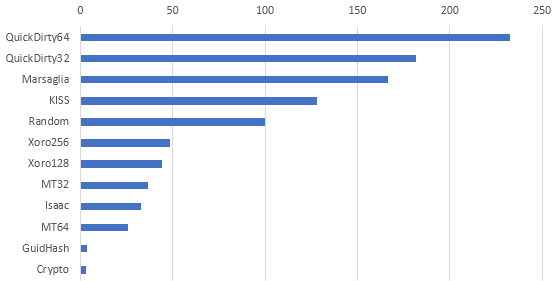
I was wondering about the relative speed of different Pseudo-Random Number Generator (PRNG) algorithms. I wrote a DOS command with methods annotated by BenchmarkDotNet attributes and gave it a run. This chart shows the relative speed of the algorithms running in a tight loop to generate 500K Int32 values. The result of each PRNG iteration was converted to an Int32 (if it wasn't one already) and added to a global Int32 so that the iterations wouldn't be optimised to nothing. The single add in each iteration should not skew the results.

Most of the algorithms are well-known and many of them are described in my Orthogonal.Common.Basic library documentation. Some observations:

• I expected the Quick 32-bit to win because it's a one-liner with one add and one truncated multiply, but the Quick 64-bit beat it for some reason.
• The Quick 64-bit is also a one-liner, but the 32-bit halves are xor'd together (which makes it a two-liner) and cast to an Int32, and despite that overhead it still wins. I suspect that this two-liner is one of the fastest reasonably good amateur PRNGs you can use.
• The Marsaglia and KISS algorithms beat the .NET Random, but they are both rather old and inferior by modern standards and are only included for historical comparison.
• The .NET Random class beats all other modern algorithms by a wide margin, even ones that are regarded as lightweight and efficient. This is quite surprising, and it might be due to some implementation details of the Knuth Subtractive algorithm that I'm not aware of. More research is needed to explain this.
• The modern Xoro algorithms are good performers, which is lucky because they're quite popular and one of them is replacing the internals of the latest .NET Random class (for more information see Random Numbers).
• I was shocked to see Guid.GetHashCode perform so poorly. It's suspicious that Guid hashes and the crypto-strong byte generator run at nearly identical speeds. This hints that the Guid uses the crypto PRNG internally, which is a question discussed in my blog post titled Guid Constant Bits.

Zip of the Visual Studio 2022 solution

Orthogonal Programming