Phone number as sum of powers

One of Dave Plummer's videos titled Top 50 Worst Computer Dialogs skims through a selection of different hilariously absurd and impractical web controls for picking dates, phone numbers, audio volume, etc.

At the 10:53 mark he shows a control where you must specify your phone number as the sum of three powers.

This intrigued me. I guessed that numbers representable in the desired form might be rather sparse up in the range of my mobile phone number which has this form (0)419XXXXXX. I wondered how sparse they were and if my phone number was one of the lucky ones. There were a few ways of tackling this question.

Random

Chose random integers for the six values in the range 1 to (say) 12 and see if a match results. This may sound stupid, but some C# script code in LINQPad can run this loop about 7 million times per second and it will quickly find a match if one exists. My phone number did not match using this technique.

Exhaustive

Loop over all combinations of the six variables to find a match. This is also stupid, because it's not only exhaustive, it's exhausting and many duplicates will occur, but I ignored that and went ahead anyway.

My C# script searched about 7 million combinations in only 10 seconds with powers up to 16 and did not find a phone number match. At this point I had proof that my phone number was not expressible in the required form.

Mathematica

I was wondering which numbers in the 9-digit range of my phone number were expressible as the sum of three powers, so I fired-up Mathematica and ran a search over distinct combinations of the six variables and tallied which numbers were expressible and in how many ways. For powers up to 16 it took about 20 seconds to produce these results in the range of my phone number:

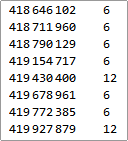
As I suspected, the expressible numbers are actually quite sparse up in this range, but it's interesting to see that certain lucky numbers can be expressed in 6 or 12 distinct ways, probably because of simple relations such as 4⁶ == 2¹².

Orthogonal Programming

WinForms RadioButton Binding

Last week I had to write demo program using Windows Forms, which was a mind-trip into the past because I migrated to using WPF for all desktop apps since 2010. As an academic exercise I tried to use data binding of the UI controls to properties of a controller class. For me, Windows Forms binding works acceptably well, but it has never felt like a first-class citizen in comparison to WPF where it's deeply integrated into the framework.

I stumbled upon an old problem that has bugged me for almost 20 years ... how to bind a group of RadioButton controls to an Enum property that represents the choices. With a fresh mind I finally solved the problem, and I've created a small sample project to preserve the code for posterity. See:

DevOps Repository - RadioBindingSample

I think it's important to point out that the original Windows Forms demo program was eventually abandoned and most of the code was migrated into a nearly identical WPF program. The Forms demo was proceeding reasonably well until more complex binding was required, and I was creating custom binding logic that was mimicking what WPF already has built-in. I had reached the same decision tipping point I had previously reached around 2009 when I realised that the powerful binding techniques available in WPF outweigh any other justifications for continuing to use Windows Forms.

Most controls in the Windows Forms namespace derive from Control which has a DataBindings property which contains a collection of binding rules. Some controls such as ToolStripItem derive from Component and do not support binding, and that's when custom binding code is required and things can get messy and convoluted. This is around the tipping point to move to WPF.

Orthogonal Programming